Predator Prey to the Heavens Read Online

Equations modelling predator–prey cycles

The Lotka–Volterra equations, also known equally the predator–prey equations, are a pair of first-order nonlinear differential equations, often used to describe the dynamics of biological systems in which two species interact, one as a predator and the other as prey. The populations change through time according to the pair of equations:

$${\displaystyle {\begin{aligned}{\frac {dx}{dt}}&=\alpha x-\beta xy,\\{\frac {dy}{dt}}&=\delta xy-\gamma y,\finish{aligned}}}$$

where

The Lotka–Volterra system of equations is an example of a Kolmogorov model,^{[i] [2] [iii]} which is a more general framework that can model the dynamics of ecological systems with predator–casualty interactions, competition, disease, and mutualism.

History [edit]

The Lotka–Volterra predator–prey model was initially proposed by Alfred J. Lotka in the theory of autocatalytic chemical reactions in 1910.^{[4] [5]} This was effectively the logistic equation,^[half-dozen] originally derived by Pierre François Verhulst.^[vii] In 1920 Lotka extended the model, via Andrey Kolmogorov, to "organic systems" using a institute species and a herbivorous fauna species as an instance^[viii] and in 1925 he used the equations to analyse predator–prey interactions in his volume on biomathematics.^[nine] The same set of equations was published in 1926 by Vito Volterra, a mathematician and physicist, who had go interested in mathematical biology.^{[5] [10] [11]} Volterra's research was inspired through his interactions with the marine biologist Umberto D'Ancona, who was courtship his daughter at the time and later was to go his son-in-police. D'Ancona studied the fish catches in the Adriatic Sea and had noticed that the percentage of predatory fish defenseless had increased during the years of World State of war I (1914–18). This puzzled him, as the fishing effort had been very much reduced during the war years. Volterra developed his model independently from Lotka and used information technology to explain d'Ancona'due south observation.^[12]

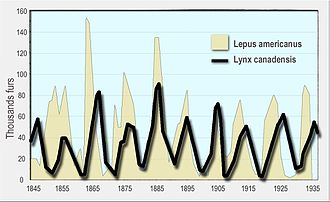
The model was afterward extended to include density-dependent prey growth and a functional response of the form developed by C. Southward. Holling; a model that has become known as the Rosenzweig–MacArthur model.^[13] Both the Lotka–Volterra and Rosenzweig–MacArthur models have been used to explicate the dynamics of natural populations of predators and prey, such as the lynx and snowshoe hare data of the Hudson'southward Bay Company^[14] and the moose and wolf populations in Isle Royale National Park.^[15]

In the late 1980s, an alternative to the Lotka–Volterra predator–casualty model (and its common-casualty-dependent generalizations) emerged, the ratio dependent or Arditi–Ginzburg model.^[sixteen] The validity of prey- or ratio-dependent models has been much debated.^[17]

The Lotka–Volterra equations take a long history of use in economical theory; their initial application is commonly credited to Richard Goodwin in 1965^[18] or 1967.^{[19] [20]}

Concrete meaning of the equations [edit]

The Lotka–Volterra model makes a number of assumptions, not necessarily realizable in nature, about the environment and development of the predator and prey populations:^[21]

1. The casualty population finds ample food at all times.
2. The food supply of the predator population depends entirely on the size of the prey population.
3. The charge per unit of change of population is proportional to its size.
4. During the process, the environment does not change in favour of ane species, and genetic adaptation is inconsequential.
5. Predators have limitless appetite.

In this case the solution of the differential equations is deterministic and continuous. This, in turn, implies that the generations of both the predator and prey are continually overlapping.^[22]

Casualty [edit]

When multiplied out, the prey equation becomes

$${\displaystyle {\frac {dx}{dt}}=\blastoff x-\beta xy.}$$

The prey are assumed to have an unlimited food supply and to reproduce exponentially, unless bailiwick to predation; this exponential growth is represented in the equation in a higher place by the term αx . The rate of predation upon the prey is assumed to exist proportional to the rate at which the predators and the prey meet, this is represented to a higher place by βxy . If either x or y is zero, then there can be no predation.

With these two terms the equation above can be interpreted as follows: the rate of change of the prey's population is given by its own growth rate minus the charge per unit at which it is preyed upon.

Predators [edit]

The predator equation becomes

$${\displaystyle {\frac {dy}{dt}}=\delta xy-\gamma y.}$$

In this equation, δxy represents the growth of the predator population. (Note the similarity to the predation rate; however, a dissimilar abiding is used, every bit the charge per unit at which the predator population grows is not necessarily equal to the charge per unit at which it consumes the prey). The term γy represents the loss rate of the predators due to either natural death or emigration, it leads to an exponential decay in the absence of prey.

Hence the equation expresses that the charge per unit of change of the predator'south population depends upon the rate at which information technology consumes prey, minus its intrinsic death charge per unit.

Solutions to the equations [edit]

The equations have periodic solutions and do not have a simple expression in terms of the usual trigonometric functions, although they are quite tractable.^{[23] [24]}

If none of the non-negative parameters α, β, γ, δ vanishes, three can be absorbed into the normalization of variables to leave merely 1 parameter: since the first equation is homogeneous in x, and the second one in y, the parameters β/α and δ/γ are absorbable in the normalizations of y and x respectively, and γ into the normalization of t, so that only α/γ remains arbitrary. It is the only parameter affecting the nature of the solutions.

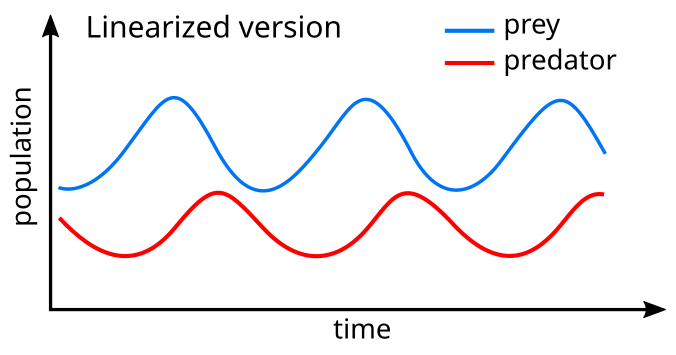
A linearization of the equations yields a solution like to unproblematic harmonic motion^[25] with the population of predators trailing that of prey past ninety° in the cycle.

A simple instance [edit]

Population dynamics for baboons and cheetahs problem mentioned bated.

Phase-space plot for the predator prey problem for various initial conditions of the predator population.

Suppose at that place are two species of animals, a baboon (prey) and a cheetah (predator). If the initial conditions are 10 baboons and x cheetahs, one tin can plot the progression of the 2 species over time; given the parameters that the growth and death rates of baboon are one.1 and 0.4 while that of cheetahs are 0.four and 0.i respectively. The selection of time interval is arbitrary.

Ane may also plot solutions parametrically every bit orbits in phase infinite, without representing time, simply with ane centrality representing the number of casualty and the other axis representing the number of predators for all times.

This corresponds to eliminating time from the two differential equations in a higher place to produce a single differential equation

${\displaystyle {\frac {dy}{dx}}=-{\frac {y}{10}}{\frac {\delta x-\gamma }{\beta y-\alpha }}}$

relating the variables x and y. The solutions of this equation are closed curves. It is acquiescent to separation of variables: integrating

${\displaystyle {\frac {\beta y-\alpha }{y}}\,dy+{\frac {\delta ten-\gamma }{10}}\,dx=0}$

yields the implicit relationship

${\displaystyle V=\delta ten-\gamma \ln(x)+\beta y-\alpha \ln(y),}$

where Five is a constant quantity depending on the initial conditions and conserved on each curve.

An aside: These graphs illustrate a serious potential problem with this as a biological model: For this specific pick of parameters, in each bicycle, the baboon population is reduced to extremely low numbers, yet recovers (while the cheetah population remains sizeable at the lowest baboon density). In real-life situations, however, take chances fluctuations of the discrete numbers of individuals, as well as the family structure and life-cycle of baboons, might cause the baboons to really go extinct, and, by consequence, the cheetahs as well. This modelling problem has been chosen the "atto-fox trouble", an atto-play a joke on being a notional 10⁻¹⁸ of a fox.^{[26] [27]}

Use of the Lambert W function yields an analytical time-dependent nonlinear solution of the equations. In add-on to time, the analytical solution also depends on the constant V, which acts a parameter, and on the initial conditions. ^{[28] [29]}. Defining normalized variables ${\displaystyle X={\frac {\delta }{\gamma }}10}$ and ${\displaystyle Y={\frac {\beta }{\gamma }}y}$ , the invariant is now ${\displaystyle Eastward={\frac {V}{\gamma }}}$ , and one obtains:

${\displaystyle X(t,E)=F_{LV}^{-1}(t,Due east)}$

${\displaystyle Y(t,E)=G_{LV}^{-ane}(t,E)}$

where the superscript ${\displaystyle -1}$ denotes the function inverse, and ${\displaystyle F_{LV}}$ and ${\displaystyle G_{LV}}$ are Lotka-Volterra integrals given by:

${\displaystyle F_{LV}^{j}(10,E)=T_{Xmin}-\int _{Xmin}^{X}{\frac {dX'}{{\frac {one}{\delta }}Ten'[1+W_{j}(\delta X'^{-\delta }eastward^{\delta (10'-East)})]}}}$

${\displaystyle G_{LV}^{j}(Y,E)=T_{Ymin}-\int _{Ymin}^{Y}{\frac {dY'}{Y'[ane+W_{j}(-Y'^{-1/\delta }east^{Y'-East})]}}}$

Here, ${\displaystyle W_{j}}$ is the Lambert W function, and the index ${\displaystyle j=0}$ or ${\displaystyle j=-1}$ denotes the associated co-operative of the office, master branch (dotted-line) and secondary branch (full line). The constants ${\displaystyle T_{Xmin}}$ and ${\displaystyle T_{Ymin}}$ are determined past initial conditions.

Analytical solutions ${\displaystyle Y(t)={\frac {\beta }{\gamma }}y(t)}$ (ruby) and ${\displaystyle Ten(t)={\frac {\delta }{\gamma }}x(t)}$ (blue) of the Lotka-Volterra system, for a value ${\displaystyle E={\frac {V}{\gamma }}=three-ln(two)\simeq 2.307}$ of the invariant, compared with numerical solutions (open symbols). The parameter is ${\displaystyle {\frac {\gamma }{\alpha }}=0.5}$ .

Phase-space plot of a further instance [edit]

A less extreme example covers:

α = 2/iii, β = 4/3, γ = 1 = δ . Assume x, y quantify thousands each. Circles correspond prey and predator initial weather condition from x = y = 0.9 to 1.viii, in steps of 0.1. The fixed indicate is at (1, 1/two).

Dynamics of the organization [edit]

In the model arrangement, the predators thrive when there are plentiful prey but, ultimately, outstrip their food supply and pass up. As the predator population is low, the prey population volition increment again. These dynamics continue in a population cycle of growth and refuse.

Population equilibrium [edit]

Population equilibrium occurs in the model when neither of the population levels is irresolute, i.eastward. when both of the derivatives are equal to 0:

$${\displaystyle x(\alpha -\beta y)=0,}$$

$${\displaystyle -y(\gamma -\delta x)=0.}$$

The to a higher place system of equations yields ii solutions:

$${\displaystyle \{y=0,\ \ x=0\}}$$

and

$${\displaystyle \left\{y={\frac {\alpha }{\beta }},\ \ x={\frac {\gamma }{\delta }}\right\}.}$$

Hence, there are two equilibria.

The showtime solution effectively represents the extinction of both species. If both populations are at 0, then they will continue to be so indefinitely. The second solution represents a fixed point at which both populations sustain their current, non-zippo numbers, and, in the simplified model, exercise so indefinitely. The levels of population at which this equilibrium is achieved depend on the chosen values of the parameters α, β, γ, and δ.

Stability of the fixed points [edit]

The stability of the fixed point at the origin can exist determined past performing a linearization using partial derivatives.

The Jacobian matrix of the predator–prey model is

$${\displaystyle J(ten,y)={\begin{bmatrix}\blastoff -\beta y&-\beta x\\\delta y&\delta 10-\gamma \end{bmatrix}}.}$$

and is known equally the customs matrix.

First stock-still point (extinction) [edit]

When evaluated at the steady state of (0, 0), the Jacobian matrix J becomes

$${\displaystyle J(0,0)={\begin{bmatrix}\alpha &0\\0&-\gamma \finish{bmatrix}}.}$$

The eigenvalues of this matrix are

$${\displaystyle \lambda _{1}=\blastoff ,\quad \lambda _{2}=-\gamma .}$$

In the model α and γ are always greater than zero, and as such the sign of the eigenvalues higher up will always differ. Hence the fixed point at the origin is a saddle betoken.

The instability of this fixed signal is of significance. If it were stable, non-zip populations might exist attracted towards it, and as such the dynamics of the organisation might atomic number 82 towards the extinction of both species for many cases of initial population levels. Notwithstanding, as the stock-still point at the origin is a saddle point, and hence unstable, it follows that the extinction of both species is difficult in the model. (In fact, this could only occur if the casualty were artificially completely eradicated, causing the predators to die of starvation. If the predators were eradicated, the prey population would abound without bound in this simple model.) The populations of prey and predator tin get infinitesimally close to zero and still recover.

Second fixed point (oscillations) [edit]

Evaluating J at the 2nd stock-still point leads to

$${\displaystyle J\left({\frac {\gamma }{\delta }},{\frac {\alpha }{\beta }}\right)={\begin{bmatrix}0&-{\frac {\beta \gamma }{\delta }}\\{\frac {\alpha \delta }{\beta }}&0\end{bmatrix}}.}$$

The eigenvalues of this matrix are

$${\displaystyle \lambda _{1}=i{\sqrt {\alpha \gamma }},\quad \lambda _{2}=-i{\sqrt {\blastoff \gamma }}.}$$

Equally the eigenvalues are both purely imaginary and cohabit to each other, this fixed point must either be a center for closed orbits in the local vicinity or an attractive or repulsive spiral. In conservative systems, there must exist airtight orbits in the local vicinity of fixed points that exist at the minima and maxima of the conserved quantity. The conserved quantity is derived above to be ${\displaystyle Five=\delta x-\gamma \ln(x)+\beta y-\alpha \ln(y)}$ on orbits. Thus orbits near the fixed betoken are closed and elliptic, and so the solutions are periodic, aquiver on a small ellipse around the fixed indicate, with a frequency ${\displaystyle \omega ={\sqrt {\lambda _{1}\lambda _{2}}}={\sqrt {\alpha \gamma }}}$ and period ${\displaystyle T=2{\pi }/({\sqrt {\lambda _{ane}\lambda _{ii}}})}$ .

Every bit illustrated in the circulating oscillations in the figure to a higher place, the level curves are closed orbits surrounding the stock-still point: the levels of the predator and prey populations cycle and oscillate without damping around the fixed point with frequency ${\displaystyle \omega ={\sqrt {\alpha \gamma }}}$ .

The value of the abiding of motility Five , or, equivalently, K = exp(−V), ${\displaystyle K=y^{\alpha }e^{-\beta y}x^{\gamma }e^{-\delta 10}}$ , can be found for the closed orbits virtually the stock-still point.

Increasing M moves a closed orbit closer to the stock-still indicate. The largest value of the constant Thousand is obtained by solving the optimization problem

$${\displaystyle y^{\alpha }e^{-\beta y}x^{\gamma }e^{-\delta ten}={\frac {y^{\alpha }x^{\gamma }}{e^{\delta 10+\beta y}}}\longrightarrow \max _{10,y>0}.}$$

The maximal value of Grand is thus attained at the stationary (fixed) bespeak ${\displaystyle \left({\frac {\gamma }{\delta }},{\frac {\alpha }{\beta }}\right)}$ and amounts to

$${\displaystyle 1000^{*}=\left({\frac {\alpha }{\beta e}}\right)^{\alpha }\left({\frac {\gamma }{\delta e}}\right)^{\gamma },}$$

where eastward is Euler's number.

See also [edit]

• Competitive Lotka–Volterra equations
• Generalized Lotka–Volterra equation
• Mutualism and the Lotka–Volterra equation
• Community matrix
• Population dynamics
• Population dynamics of fisheries
• Nicholson–Bailey model
• Reaction–diffusion arrangement
• Paradox of enrichment
• Lanchester's laws, a similar arrangement of differential equations for military forces

Notes [edit]

1. ^ Freedman, H. I. (1980). Deterministic Mathematical Models in Population Ecology. Marcel Dekker.
2. ^ Brauer, F.; Castillo-Chavez, C. (2000). Mathematical Models in Population Biology and Epidemiology. Springer-Verlag.
3. ^ Hoppensteadt, F. (2006). "Predator-prey model". Scholarpedia. 1 (10): 1563. Bibcode:2006SchpJ...1.1563H. doi:10.4249/scholarpedia.1563.
4. ^ Lotka, A. J. (1910). "Contribution to the Theory of Periodic Reaction". J. Phys. Chem. 14 (three): 271–274. doi:10.1021/j150111a004.
5. ^ ^{a b} Goel, N. S.; et al. (1971). On the Volterra and Other Nonlinear Models of Interacting Populations. Academic Printing. ISBN0-12-287450-1.
6. ^ Berryman, A. A. (1992). "The Origins and Evolution of Predator-Prey Theory" (PDF). Ecology. 73 (five): 1530–1535. doi:x.2307/1940005. JSTOR 1940005. Archived from the original (PDF) on 2010-05-31.
7. ^ Verhulst, P. H. (1838). "Notice sur la loi que la population poursuit dans son accroissement". Corresp. Mathématique et Physique. 10: 113–121.
8. ^ Lotka, A. J. (1920). "Analytical Note on Certain Rhythmic Relations in Organic Systems". Proc. Natl. Acad. Sci. UsaA. 6 (seven): 410–415. Bibcode:1920PNAS....6..410L. doi:10.1073/pnas.6.7.410. PMC1084562. PMID 16576509.
9. ^ Lotka, A. J. (1925). Elements of Physical Biological science. Williams and Wilkins.
10. ^ Volterra, V. (1926). "Variazioni e fluttuazioni del numero d'individui in specie animali conviventi". Mem. Acad. Lincei Roma. 2: 31–113.
11. ^ Volterra, 5. (1931). "Variations and fluctuations of the number of individuals in animal species living together". In Chapman, R. N. (ed.). Animal Ecology. McGraw–Colina.
12. ^ Kingsland, Due south. (1995). Modeling Nature: Episodes in the History of Population Ecology. University of Chicago Press. ISBN978-0-226-43728-half-dozen.
13. ^ Rosenzweig, G. Fifty.; MacArthur, R.H. (1963). "Graphical representation and stability atmospheric condition of predator-casualty interactions". American Naturalist. 97 (895): 209–223. doi:10.1086/282272. S2CID 84883526.
14. ^ Gilpin, M. E. (1973). "Exercise hares swallow lynx?". American Naturalist. 107 (957): 727–730. doi:10.1086/282870. S2CID 84794121.
15. ^ Jost, C.; Devulder, G.; Vucetich, J.A.; Peterson, R.; Arditi, R. (2005). "The wolves of Island Royale brandish calibration-invariant satiation and density dependent predation on moose". J. Anim. Ecol. 74 (5): 809–816. doi:x.1111/j.1365-2656.2005.00977.x.
16. ^ Arditi, R.; Ginzburg, L. R. (1989). "Coupling in predator-prey dynamics: ratio dependence" (PDF). Journal of Theoretical Biology. 139 (3): 311–326. doi:10.1016/s0022-5193(89)80211-5.
17. ^ Abrams, P. A.; Ginzburg, L. R. (2000). "The nature of predation: prey dependent, ratio dependent or neither?". Trends in Environmental & Evolution. 15 (8): 337–341. doi:10.1016/s0169-5347(00)01908-x. PMID 10884706.
18. ^ Gandolfo, G. (2008). "Giuseppe Palomba and the Lotka–Volterra equations". Rendiconti Lincei. nineteen (4): 347–357. doi:10.1007/s12210-008-0023-7. S2CID 140537163.
19. ^ Goodwin, R. Thou. (1967). "A Growth Cycle". In Feinstein, C. H. (ed.). Socialism, Capitalism and Economic Growth. Cambridge University Press.
20. ^ Desai, M.; Ormerod, P. (1998). "Richard Goodwin: A Short Appreciation" (PDF). The Economic Periodical. 108 (450): 1431–1435. CiteSeerXx.i.i.423.1705. doi:10.1111/1468-0297.00350. Archived from the original (PDF) on 2011-09-27. Retrieved 2010-03-22 .
21. ^ "PREDATOR-Casualty DYNAMICS". www.tiem.utk.edu . Retrieved 2018-01-09 .
22. ^ Cooke, D.; Hiorns, R. Westward.; et al. (1981). The Mathematical Theory of the Dynamics of Biological Populations. Vol. 2. Bookish Press.
23. ^ Steiner, Antonio; Gander, Martin Jakob (1999). "Parametrische Lösungen der Räuber-Beute-Gleichungen im Vergleich". Il Volterriano. 7: 32–44.
24. ^ Evans, C. M.; Findley, G. L. (1999). "A new transformation for the Lotka-Volterra problem". Journal of Mathematical Chemical science. 25: 105–110. doi:10.1023/A:1019172114300. S2CID 36980176.
25. ^ Tong, H. (1983). Threshold Models in Non-linear Time Serial Analysis. Springer–Verlag.
26. ^ Lobry, Claude; Sari, Tewfik (2015). "Migrations in the Rosenzweig-MacArthur model and the "atto-fox" trouble" (PDF). Arima. 20: 95–125.
27. ^ Mollison, D. (1991). "Dependence of epidemic and population velocities on bones parameters" (PDF). Math. Biosci. 107 (two): 255–287. doi:10.1016/0025-5564(91)90009-8. PMID 1806118.
28. ^ Leconte, M.; Masson, P.; Qi, Fifty. (2022). "Limit cycle oscillations,response fourth dimension,and the time-dependent solution to the Lotka-Volterra predator-casualty model". Physics of Plasmas. 29: 022302. doi:10.1063/5.0076085.
29. ^ Leconte, Yard.; Masson, P.; Qi, 50. (2022). "Limit bike oscillations,response time,and the fourth dimension-dependent solution to the Lotka-Volterra predator-prey model". Arxiv: 2110.11557. doi:10.48550/arXiv.2110.11557.

Farther reading [edit]

• Hofbauer, Josef; Sigmund, Karl (1998). "Dynamical Systems and Lotka–Volterra Equations". Evolutionary Games and Population Dynamics. New York: Cambridge Academy Press. pp. ane–54. ISBN0-521-62570-Ten.
• Kaplan, Daniel; Glass, Leon (1995). Understanding Nonlinear Dynamics . New York: Springer. ISBN978-0-387-94440-one.
• Leigh, E. R. (1968). "The ecological role of Volterra's equations". Some Mathematical Problems in Biology. – a modern discussion using Hudson'southward Bay Company data on lynx and hares in Canada from 1847 to 1903.
• Murray, J. D. (2003). Mathematical Biology I: An Introduction. New York: Springer. ISBN978-0-387-95223-ix.

External links [edit]

• From the Wolfram Demonstrations Project — requires CDF player (costless):
  • Predator–Prey Equations
  • Predator–Prey Model
  • Predator–Prey Dynamics with Type-Ii Functional Response
  • Predator–Casualty Ecosystem: A Real-Time Amanuensis-Based Simulation
• Lotka-Volterra Algorithmic Simulation (Web simulation).

stevensrhisfor.blogspot.com

Source: https://en.wikipedia.org/wiki/Lotka%E2%80%93Volterra_equations

Share this post